As a high school or undergraduate Mathematics teacher, you can use this set of computer-based tools to help you in teaching topics such as Differentiation, Derivatives of Polynomials, and Tangent Line Problems in Introductory Calculus.
This lesson plan allows students to perform polynomial differentiation and solve tangent line problems using climate data such as atmospheric CO2 concentrations data since 1950.
Thus, the use of this lesson plan allows you to integrate the teaching of a climate science topic with a core topic in Mathematics.
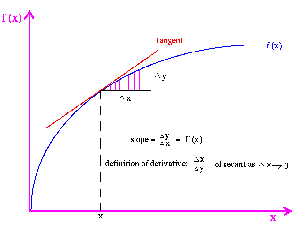
The tools in this lesson plan will enable students to:
This activity will help students to:
Here is a step-by-step guide to using this lesson plan in the classroom/laboratory. We have suggested these steps as a possible plan of action. You may customize the lesson plan according to your preferences and requirements.
(video)
Use this lesson plan to help your students find answers to:
| 1 | Visualization | An interactive visualization, “Interactive Graph showing Differentiation of a Polynomial Function” from Interactive Mathematics: This can be accessed here. |
| 1 | Reading, “Derivatives of Polynomials” | World Web Math, Massachusetts Institute of Technology |
| 2 | Micro-lecture (video), “Differentiating polynomials” | Khan Academy |
| 3 | Classroom/Laboratory Activity , “Mauna Loa Yearly Average CO2” | Thomas J. Pfaff,Sustainability Math |
| 3 | Additional Resource | Interactive Mathematics |
Here is a step-by-step guide to using this lesson plan in the classroom/laboratory. We have suggested these steps as a possible plan of action. You may customize the lesson plan according to your preferences and requirements.
Reading and Associated Activity (30 – 60 min)
Classroom/Laboratory activity (~60 min)
Then, help your students apply the learned concepts through a hands-on classroom/laboratory activity, “U.S. and China CO2 Emissions”, by Thomas J. Pfaff at Sustainability Math. This activity uses CO2 emission data and population data for the U.S. and China for the period 1980 to 2015.
Suggested questions/assignments for learning evaluation
Use the tools and the concepts learned so far to discuss and determine answers to the following questions:
Use this lesson plan to help your students find answers to:
| 1 | Videos | Video tutorial, “Riemann sums”, from Khan Academy: This can be accessed here. |
| 1 | Reading and Associated Activity, “Calculating the area under a curve using Riemann sums” | D. Q. Nykamp; from Math Insight |
| 2 | Classroom/Laboratory Activity, “U.S. and China CO2 Emissions | Thomas J. Pfaff, Sustainability Math |
| 3 | Additional Resources | Khan Academy |
All maps & pedagogical tools are owned by the corresponding creators, authors or organizations as listed on their websites. Please view the individual copyright and ownership details for each tool using the links provided. We do not claim ownership of or responsibility or liability for any of these tools. Images copyrights remain with the respective owners.
TROP ICSU is a project of the International Union of Biological Sciences and Centre for Sustainability, Environment and Climate Change, FLAME University.