As a high school or undergraduate Mathematics teacher, you can use this set of computer-based tools to help you in teaching introductory differential calculus and specifically polynomial differentiation.
This lesson plan will allow you to teach introductory derivatives and differentiation. The lesson plan includes a hands-on computer-based classroom activity to be conducted on a dataset of global annual mean surface air temperatures from 1880 to 2018. This activity includes a set of inquiry-based questions that will enable your students to apply their understanding of function composition and polynomial differentiation and to solve tangent line problems.
Thus, the use of this lesson plan allows you to integrate the teaching of a climate science topic with a ore topic in Mathematics.
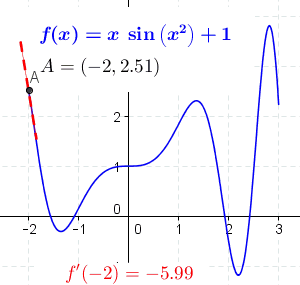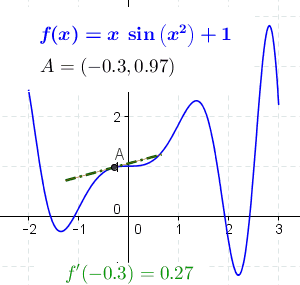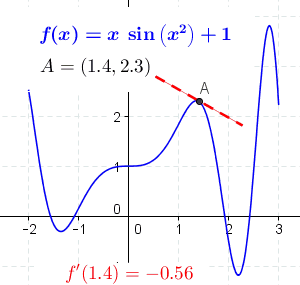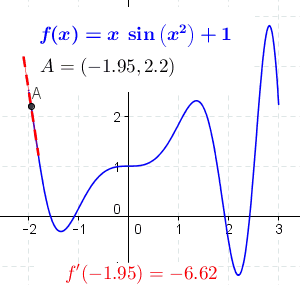
The tools in this lesson plan will enable students to:
Here is a step-by-step guide to using this lesson plan in the classroom/laboratory. We have suggested these steps as a possible plan of action. You may customize the lesson plan according to your preferences and requirements.
Teaching Module(30 min)
Use the teaching module, ‘Differentiation: definition and basic derivative rules’ by Khan Academy, to introduce the concept of derivatives and differentiation.
Navigate to the sub-sections within the module to explain derivative rules, the power rule, and how to differentiate polynomials.
Use the in-built practice exercises and quizzes to evaluate your students’ understanding of the topics.
Classroom/ Laboratory activity(20 min)
Use the classroom activity, ‘Global Average Temperature’ from Sustainability Math by Thomas J. Pfaff, Professor of Mathematics, Ithaca College, USA, to enable your students to apply their understanding of derivatives and polynomial differentiation using a dataset from NASA Goddard Institute for Space Studies (GISS).
This classroom activity includes a dataset of the global annual mean surface air temperature linked from NASA’s observations from 1950 to 2018. It also includes data from 1880 to 2018.This data is provided in an Excel spreadsheet.
The classroom activity also includes a Word document that contains directions on how to use different mathematical methods on the data provided.
It further includes questions that you may wish to use in your classroom to explain mathematical functions and methods and to initiate a discussion on the increase in global annual mean surface temperature due to anthropogenically forced global warming.
Direct your students to download the Excel file (with dataset) and the Word document (with directions to use the dataset and a set of questions to analyze the dataset).
Proceed with the classroom activity and encourage your students to answer the questions by applying their understanding of function composition, tangent line equation, and polynomial differentiation.
Visualizations(10 min)
Use the visualizations, ‘Global Temperature’ by NASA/GISS, ‘Temperature Change; 1880-2019’ by Antti Lipponen using NASA GISTEMP data, and ‘Simulated global temperature change’ by US Geological Survey (USGS) to encourage discussion amongst your students about the real and simulated increase of global surface air temperatures from the years 1880-2020 and 1850-2100 respectively. Discuss how these changes could be affecting Earth’s climate in recent times.
Use this lesson plan to help your students find answers to:
| 1 | Teaching Module; ‘Differentiation: definition and basic derivative rules’ | Developed by Khan Academy |
| 2 | Teaching Module; ‘Derivatives and the Shape of a Graph’ | Provided by Sustainability Math by Thomas J. Pfaff, Professor of Mathematics, Ithaca College, USA |
| 3 | Visualizations | ‘Global Temperature’ by NASA: Climate Change and Global Warming ‘Temperature Change; 1880-2019’ by Antti Lipponen using NASA GISTEMP data ‘Simulated global temperature change’ by US Geological Survey (USGS) |
Here is a step-by-step guide to using this lesson plan in the classroom/laboratory. We have suggested these steps as a possible plan of action. You may customize the lesson plan according to your preferences and requirements.
Teaching Module(30 min)
Use the teaching module, ‘Differentiation: definition and basic derivative rules’ by Khan Academy, to introduce the concept of derivatives and differentiation.
Navigate to the sub-sections within the module to explain derivative rules, the power rule, and how to differentiate polynomials.
Use the in-built practice exercises and quizzes to evaluate your students’ understanding of the topics.
Classroom/ Laboratory activity(20 min)
Use the classroom activity, ‘Global Average Temperature’ from Sustainability Math by Thomas J. Pfaff, Professor of Mathematics, Ithaca College, USA, to enable your students to apply their understanding of derivatives and polynomial differentiation using a dataset from NASA Goddard Institute for Space Studies (GISS).
This classroom activity includes a dataset of the global annual mean surface air temperature linked from NASA’s observations from 1950 to 2018. It also includes data from 1880 to 2018.This data is provided in an Excel spreadsheet.
The classroom activity also includes a Word document that contains directions on how to use different mathematical methods on the data provided.
It further includes questions that you may wish to use in your classroom to explain mathematical functions and methods and to initiate a discussion on the increase in global annual mean surface temperature due to anthropogenically forced global warming.
Direct your students to download the Excel file (with dataset) and the Word document (with directions to use the dataset and a set of questions to analyze the dataset).
Proceed with the classroom activity and encourage your students to answer the questions by applying their understanding of function composition, tangent line equation, and polynomial differentiation.
Visualizations(10 min)
Use the visualizations, ‘Global Temperature’ by NASA/GISS, ‘Temperature Change; 1880-2019’ by Antti Lipponen using NASA GISTEMP data, and ‘Simulated global temperature change’ by US Geological Survey (USGS) to encourage discussion amongst your students about the real and simulated increase of global surface air temperatures from the years 1880-2020 and 1850-2100 respectively. Discuss how these changes could be affecting Earth’s climate in recent times.
Use this lesson plan to help your students find answers to:
| 1 | Teaching Module; ‘Differentiation: definition and basic derivative rules’ | Developed by Khan Academy |
| 2 | Teaching Module; ‘Derivatives and the Shape of a Graph’ | Provided by Sustainability Math by Thomas J. Pfaff, Professor of Mathematics, Ithaca College, USA |
| 3 | Visualizations |
‘Global Temperature’ by NASA: Climate Change and Global Warming
‘Temperature Change; 1880-2019’ by Antti Lipponen using NASA GISTEMP data‘Simulated global temperature change’ by US Geological Survey (USGS) |
